การคูณเมทริกซ์และค่าคงที่
กำหนดเมทริกซ์  และจำนวน
และจำนวน  เราสามารถนิยาม
เราสามารถนิยาม
 และจำนวน
และจำนวน  เราสามารถนิยาม
เราสามารถนิยาม ผลคูณสเกลาร์  ว่าเป็นเมทริกซ์ขนาด
ว่าเป็นเมทริกซ์ขนาด 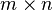 ที่คำนวณ
ที่คำนวณ
 ว่าเป็นเมทริกซ์ขนาด
ว่าเป็นเมทริกซ์ขนาด 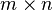 ที่คำนวณ
ที่คำนวณ โดยการนำ  ไปคูณสมาชิกแต่ละตัวของ
ไปคูณสมาชิกแต่ละตัวของ  กล่าวคือ
กล่าวคือ
 ไปคูณสมาชิกแต่ละตัวของ
ไปคูณสมาชิกแต่ละตัวของ  กล่าวคือ
กล่าวคือ หาก  แล้ว
แล้ว 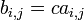 ยกตัวอย่างเช่น
ยกตัวอย่างเช่น
 แล้ว
แล้ว 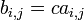 ยกตัวอย่างเช่น
ยกตัวอย่างเช่น จะเห็นว่า ปฏิบัติการทั้งสองข้างต้น (การบวกและการคูณด้วยสเกลาร์)
ช่วยให้เราสามารถมองเมทริกซ์ขนาด 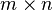 ว่าเป็นเวกเตอร์ที่มีมิติ
ว่าเป็นเวกเตอร์ที่มีมิติ  ด้วยเหตุนี้ เซตของเมทริกซ์ที่มีขนาดเท่ากับจึงเป็นปริภูมิเวกเตอร์ชนิดหนึ่ง
ด้วยเหตุนี้ เซตของเมทริกซ์ที่มีขนาดเท่ากับจึงเป็นปริภูมิเวกเตอร์ชนิดหนึ่ง
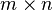 ว่าเป็นเวกเตอร์ที่มีมิติ
ว่าเป็นเวกเตอร์ที่มีมิติ  ด้วยเหตุนี้ เซตของเมทริกซ์ที่มีขนาดเท่ากับจึงเป็นปริภูมิเวกเตอร์ชนิดหนึ่ง
ด้วยเหตุนี้ เซตของเมทริกซ์ที่มีขนาดเท่ากับจึงเป็นปริภูมิเวกเตอร์ชนิดหนึ่ง
ไม่มีความคิดเห็น:
แสดงความคิดเห็น